Sometimes the way to solve a geolocation challenge is obvious. Other times less so. The Quiztime challenge that Fiete Stegers set on 8th October was certainly in the latter category and was probably the hardest Quiztime I’ve attempted so far.
This is quite a lengthy write-up, so click to skip ahead to sections of interest.
- Investigation Model
- Finding the Plane
- Finding the Location
- Using Automation
- Build A Timeline
- Overpass Query
- Speed and Scale With Google Earth
- Who Was The Commander?
Investigation Model
What makes this challenge so difficult? Overall the biggest challenge is that the image appears to lack detailed information: the plane we need to identify is small and blurry and the location does not have any features that are readily identifiable. We cannot even begin to answer the third question about the operational commander until the first two questions are solved, so overall these seems like a very tough challenge to solve. Nonetheless it can be solved even with the small amount of information we have to being with.
But how to get started when the amount of information available seems so small? In an OSINT challenge like this one it is essential to take a systematic approach to make sure that your research starts in the right way and that you stay on track throughout. If you just threw a few of your favourite tools at this challenge you probably ran out of lines of enquiry quite quickly. Even if you didn’t it is very easy to get stuck down so many rabbit holes that you begin to become discouraged and give up.
It is easy to get overwhelmed by the apparent lack of easy options and seemingly endless enquiries that go nowhere. To counter these problems investigators have designed various models that make it easier for research to remain structured and effective. I’ve written many times about gap analysis, which is a clear, simple structure that helps with decision making as an investigation progresses. It forces you to continually refocus on what you are actually trying to achieve and avoid speculative enquiries that drag you down too many rabbit holes.
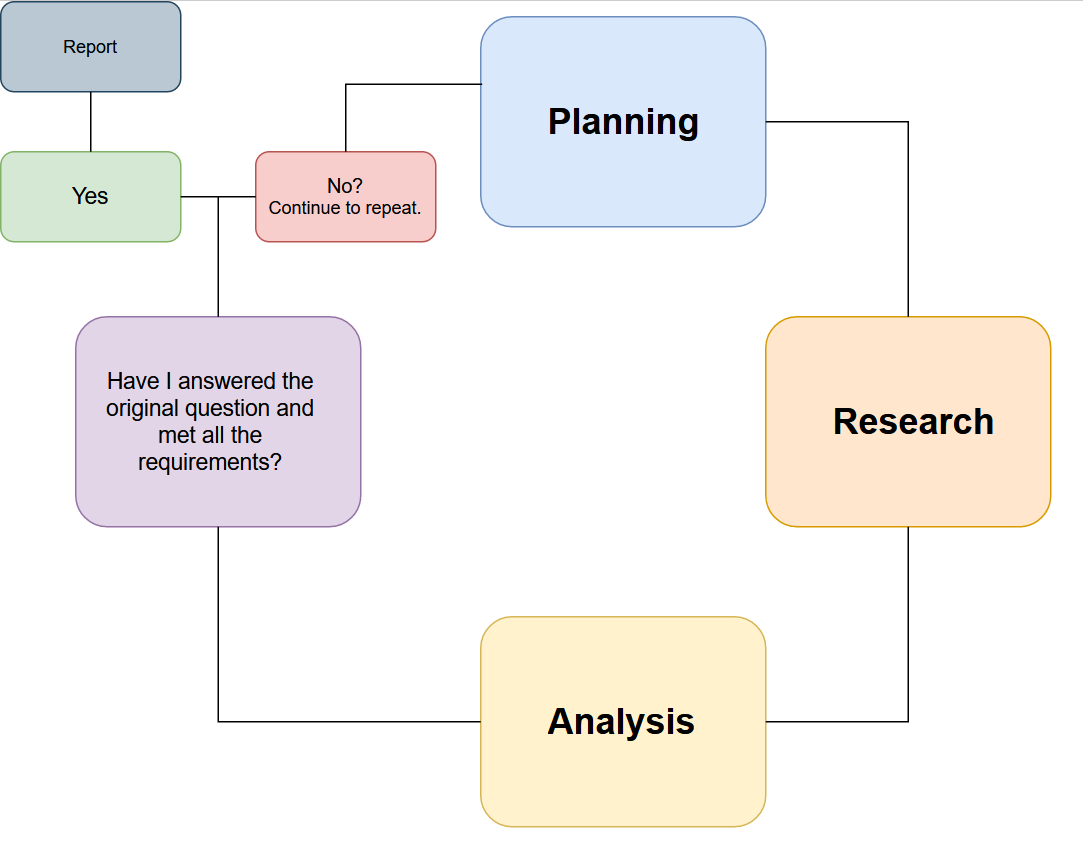
Gap analysis is really a simplification of the Intelligence Cycle (see above). We start with our requirements and initial parameters and ask What do I know? and What does this mean? Often the answer these questions at the early stage of a challenge like this is “not much”. This shouldn’t be too concerning because the next question we have to ask is “what do I need to know?” Answering this question is what gets an investigation out of the starting blocks and determines what we will research first.
Finally we ask “How do I find out?” – this is the stage where we can think about tooling and which resources we can make use of as we actually gather the information we need.
This is also the stage where inexperienced investigators can go wrong, because they choose a selection of favourite tools and techniques and try to apply them to the case. If the tool works, that’s great, but if the tool doesn’t work or doesn’t find the data you need then you will not be successful. There’s no point spending time and money on OSINT tools and services unless you also understand how they fit into the wider requirements of a successful investigation. Structure first, tools second.
After gathering the information that we need, we have to analyse it. Have we actually answered the questions we set out to answer at the start? If we have then we can report our findings and finish. If we haven’t then we just return to the start of our cycle armed with the new information we discovered – what do I know? What does this mean? What do I need to know? How do I find out? And so on, and so on until we finally answer the questions we set out to answer in the first place.
This model ensures that investigations start and continue with a firm footing. I don’t intend to refer to it constantly throughout the rest of this write-up but when I say things like “we need to know” or “this means that” or if I describe a resource that will find a particular type of information then this is then process that I have in mind.
Anyway, let’s start by finding a plane…
Finding the Plane
Where to start with identifying the aeroplane in the picture? It doesn’t look much like a typical airliner. The wings appear quite high and the paint scheme is quite dark. This doesn’t automatically determine the type of aircraft of course, but there is a clue in Fiete’s question when he asks who the commander of the operation is. This language indicates that the aircraft is more likely to be military rather than civilian.

This is a mixed blessing. If the plane is military then the pool of possible aircraft types is relatively small, which will make identification easier. The downside is that military flights are generally not recorded by sites that log ADSB data, like Flightradar. This means it won’t be possible to identify the aircraft and then find a record of its flight path and then work out the location and the mission.
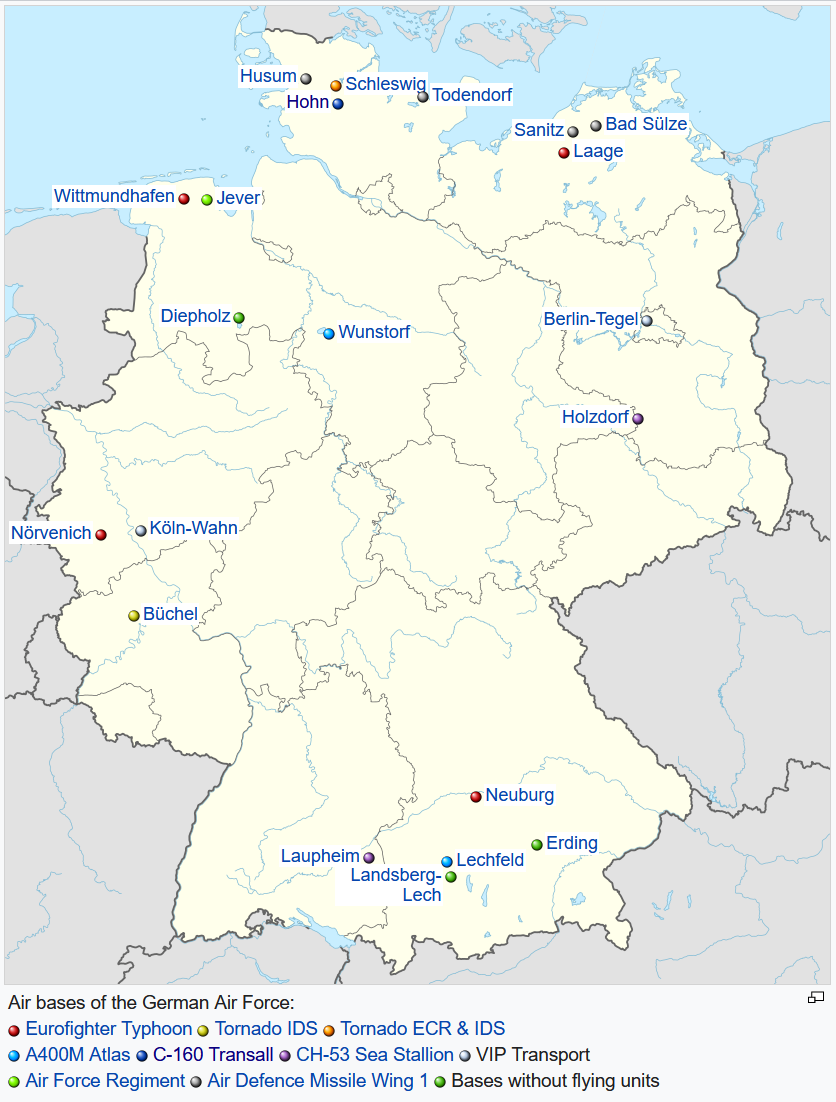
So how to identify the military plane? We can work on the basis that Fiete is based in Germany, so we can start by looking at the type of aircraft the German Air Force uses and see if any of them match. This article summarises the main types nicely. There’s also a helpful Wikipedia article that lists all the types of aircraft the GAF has ever flown. The aircraft Fiete saw is clearly not a jet combat aircraft like the Eurofighter or Tornado, it isn’t a helicopter or airliner. This really leaves only two possibilities from the list: the A400M or the Transall C-160.
With such a small low-quality image to work from, this is quite a difficult challenge. Fortunately Bellingcat’s Timmi Allen provided an enhanced version of the image which has just enough detail to confirm the aircraft type.

The key difference between the A400M and C-160 can be seen around the tailfin. On the A400M the elevators sit on top of the tailfin.

On the C-160, they are lower down at the base of the tail.

So it is most likely that this aircraft is a German Air Force C-160. This video from May 2021 shows a C-160 flying in formation with an A-400M, so spotting the difference between them is much easier. We’ve only solved a small part of the problem though. This quiz requires a lot a very precise information: we don’t just need to know that this was any C-160, we need to know the exact plane, because we also need to know the exact location and exact operation this aircraft was involved in when Fiete photographed it.
So how could the C-160 be identified? Finding out about military aircraft is not as hard as you might think. The existence of very active planespotting communities like Scramble.nl or Planespotters.net means that there are often detailed records and photographs of military aircraft movements. So what can they tell us?
A brief search around Wikipedia shows us that the GAF C-160 fleet was based only at Hohn, in Schleswig-Holstein, so this will be something to consider when we try to find the location later on. More importantly there is a message board at Scramble.nl dedicated solely to news about Hohn Air Base and its C-160 fleet. The 2021 thread is only three pages long, but from it we learn that unit LTG63 are based there and that throughout this year they have been slowly preparing for the final retirement of their C-160 fleet. From 14 aircraft at the start of the year, only 6 remained in service by September. This also means we have to identify just one aircraft from a possible 6. Given that Germany had 110 of these aircraft in service at one time, this makes our task a little easier.
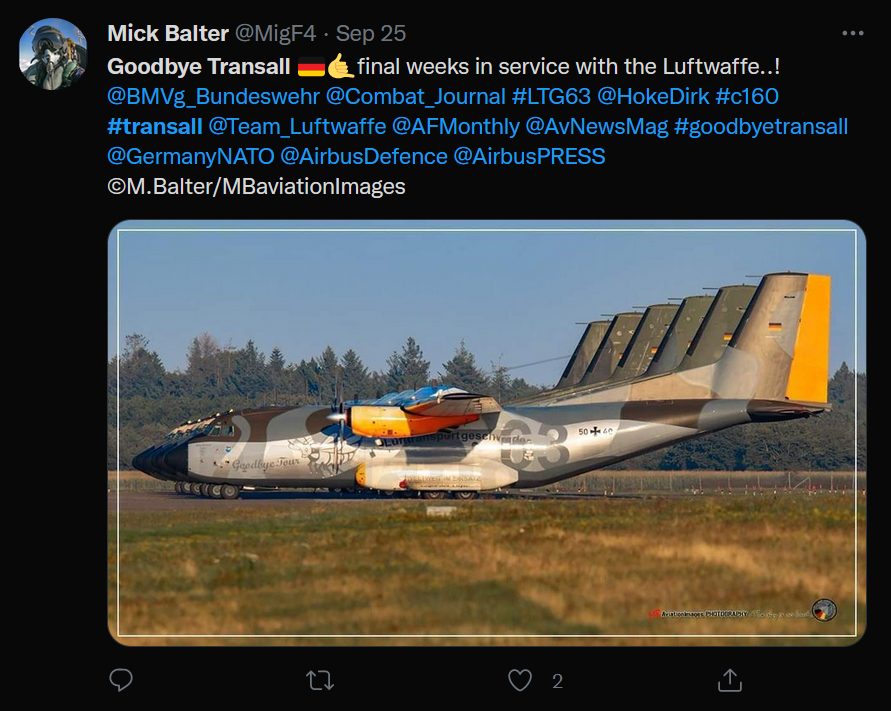
Scramble also tells us that there was a special celebration day for the C-160 at Hohn on 23rd September. Thankfully the planespotting community documented this “Goodbye Transall” event very thoroughly. This YouTube video of the event shows all six of the remaining C-160 aircraft in service.

From the information on Scramble and from the video footage it becomes clear that one of the C-160 aircraft received special paint markings to celebrate the end of the C-160’s service. This aircraft has the serial number 50+40 and has distinctive orange markings on the tail and engines. A second look at Timmi’s enhanced image also shows that the aircraft had a distinctive orange mark on the tail, so it is quite possible that the aircraft Fiete saw is C-160 50+40, which is nicknamed “Retrobrummel“. By late September it was certainly the only C-160 in the fleet that had this distinctive marking.
There’s still too much assumption here for my liking though, and we will still need to verify that the plane is 50+40 rather than simply speculating. We also need to consider how we could be certain of the plane’s identity if Timmi had not provided the enhanced image. It is slightly more time consuming, but still possible.

For example, searching for “Transall C-160D” on Planespotters.net gives a collection of images that we can sort by date taken. It becomes clear that in the final few weeks of the C-160’s service, 50+40 Retrobrummel was more active than any other C-160 (or at least it was photographed more – but was this due to its special paint scheme?). This data is incomplete and we cannot be certain that every active C-160 movement was documented by planespotters, but from the information that is available, 50+40 seems to have been far more active than any other C-160 during the time leading up to Fiete’s quiz.
The time is important too. So far we only know that Fiete posted the quiz on October 8th and that he took the image “recently”, so we will also have to have a more specific time frame in mind before we can be certain of our answers.
There are more questions to answer before we can be certain about the plane’s identity, but for now we will test out the hypothesis that Fiete saw the C-160 50+40 “Retrobrummel”.
Finding The Location
Finding the location that Fiete took the photograph from was prolonged and difficult, but it is possible. We now have a hypothesis for the identity of the plane, but we still need to know to where Fiete was and the exact operation the plane was involved in. Although there is still much uncertainty at this stage, we can be certain of one thing: Fiete and the plane were in the same place at the same time, so we can either use the plane to find Fiete, or we can use Fiete to find the plane.
If this was a civilian plane we could grab the GPS coordinates of routes it had recently flown and then work from there to find the location. This can be very effective, but we are dealing with a military plane so we won’t be able to get any GPS data. This means that working from the plane to find Fiete is not likely to be successful.

The second issue is that the landscape lacks any really distinctive features. There is a cell tower, a recently harvested field, a road, and a set of 6 floodlights in the background. As tough as it might seem, this will actually be enough information to find where Fiete was standing when he photographed the plane. So we will be able to work from Fiete’s location to find the target aircraft.
So where was Fiete? We know from his Twitter bio that he is usually based in Hamburg, but this location looks very rural and isn’t in a city. We know there is a cell tower in a field, but there probably thousands of such locations in Germany and we need to find one specific mast. There are sites like Handymasten that list every cell tower in Germany, but by itself this resource is no good if we don’t have an approximate location to focus on.
Using Automation
Finding one aircraft from a possible six is not too difficult – but how do you find one cell tower among tens of thousands? This is far too difficult a task to perform manually. In theory you could look up every cell mast in Germany with Handymasten and then try to verify the location with Google Maps, but given the average human life expectancy is only about 73 you would most likely die (of boredom) before successfully completing the task.
Working with large amounts of data is impossible without some degree of automation. To find Fiete’s location I used two different automation techniques. Firstly I used Overpass Turbo to find all the possible cell towers, and secondly I used Google Earth to make a high-speed KML tour of all the possible locations until I found one with the right features. In total it took about an hour to find the location instead of a lifetime.
Overpass Turbo allows API access to Open Street Map. If you haven’t used Overpass Turbo before I’ve written a couple of introductory tutorials here and here that cover the basics, but the main advantage is that it can find thousands of geographic features in a very small amount of time.
Since cell phone sites are recorded in Open Street Map, we just need to write a query that will plot the locations of all the cell towers in a given area. Sounds easy enough, but there is just one problem – which area is Fiete in? Until we know roughly where he is then there is no point generating a map of cell towers to look at or the task will be too overwhelming. So before running an Overpass query we need a rough idea where Fiete was, even if we do not know the precise location.
We already know Fiete is based in Hamburg, and we know he posted his quiz on October 8th with a “recent” photograph, so we can work with this information. One technique to learn more about a photograph is to learn more about the person who took it by exploring their digital shadow. Generally I don’t like to rely on this approach for Quiztime because it always feels a little intrusive, but in this case it was necessary. Fiete’s Twitter account gave no other clues as to where he might have been in the period leading up to 8th October – but does he have any other social media accounts that might provide a clue?
It turns out that he does. Fiete also has an open Instagram account that we can look at to learn about where he might have been.
Build A Timeline
Constructing a timeline is an extremely useful technique for seeing where intelligence subjects overlap. If we can construct a timeline for Fiete and a second timeline for C-160 50+40 and find where they overlap (if they do overlap that is) then we can probably confirm the identity of the plane and also the mission it was on at the time. Let’s start with Fiete’s timeline in the run up to the quiz:
30th Sept 2021: Barmbeker Markt in Hamburg.
1st Oct 2021: Aldi, location unknown.
4th Oct 2021: A silo. Location unknown but looks rural.
5th Oct 2021: A sugar beet crop. Location unknown, but probably rural.
6th Oct 2021: A restaurant somewhere.
7th Oct 2021: Near the sea or a large lake.
8th Oct 2021: Standing on a drain cover, location unknown.
It looks like Fiete had a little trip away from Hamburg in the week leading up to the quiz. If we can find out roughly where any of these places are, then we know where to start a query for cell towers with Overpass Turbo. By paying close attention to the images Fiete posted it is actually possible to work out the area of Germany he was in. Geolocating the silo or the restaurant is probably too time consuming, but consider this image that Fiete posted on October 8th:

What are we looking at? It’s a drain cover – but it has a coat of arms on it. If we can find out what the coat of arms relates to we can probably work out roughly which area of Germany Fiete was in. Yandex is the best reverse image search engine for finding direct likenesses, so by querying Yandex for drain covers that match the one Fiete posted, we might be able to find the location. Sure enough in the results we can see that the symbol on the drain cover matches that for the German town of Eckernförde. Bingo!
Overpass Query
Now we know that Fiete was in the Eckernförde area in the time leading up the the quiz, we can focus our search for phone masts in this area. In Overpass Turbo a query to find phone masts looks something like this:
(
node["tower:type"="communication"]({{bbox}});
node["man_made"="tower"]({{bbox}});
node["communication:mobile_phone"="yes"]({{bbox}});
node["tower:construction"="lattice"]({{bbox}});
node["communication:mobile"="yes"]({{bbox}});
node["mast:type"="communication"]({{bbox}});
node["mast:type"="column"]({{bbox}});
node["mast:type"="telecommunication"]({{bbox}});
node["mast:type"="lattice"]({{bbox}});
node["mast:type"="mobile_phone"]({{bbox}});
)->.towers;
node.towers;
out;This query tells Overpass to return any node in its database that matches one of the descriptive tags relating to mobile phone masts. I added in a very broad range of tags because I have found that sometimes naming conventions for mobile masts were inconsistent and some masts might have been left out. All the possible node types are grouped together in a group called towers.
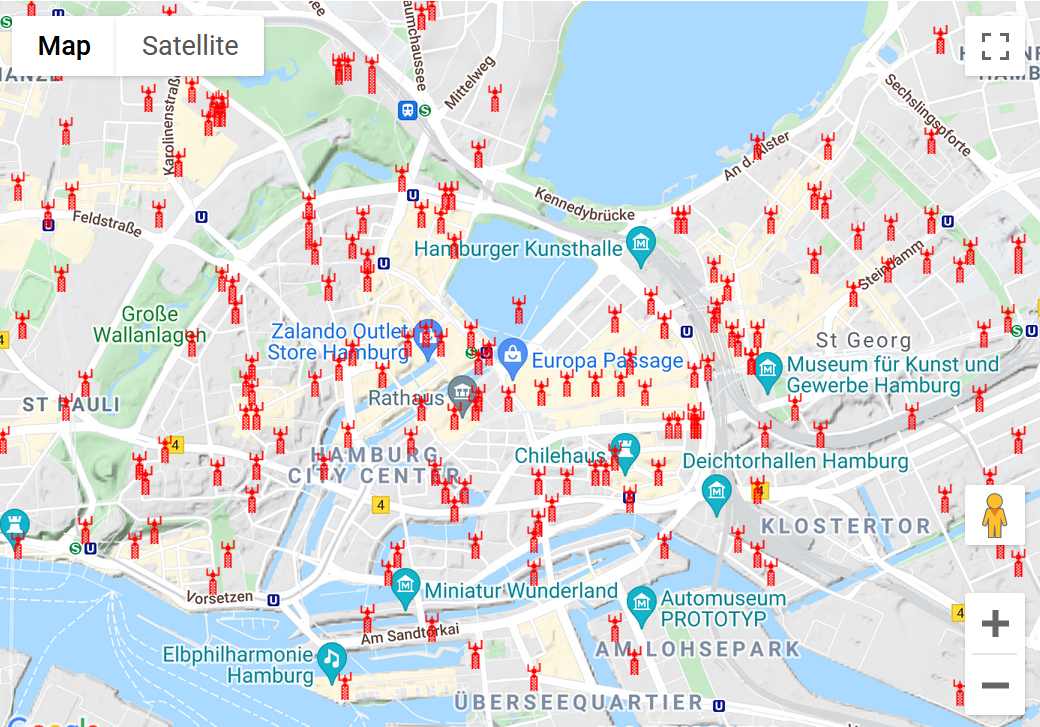
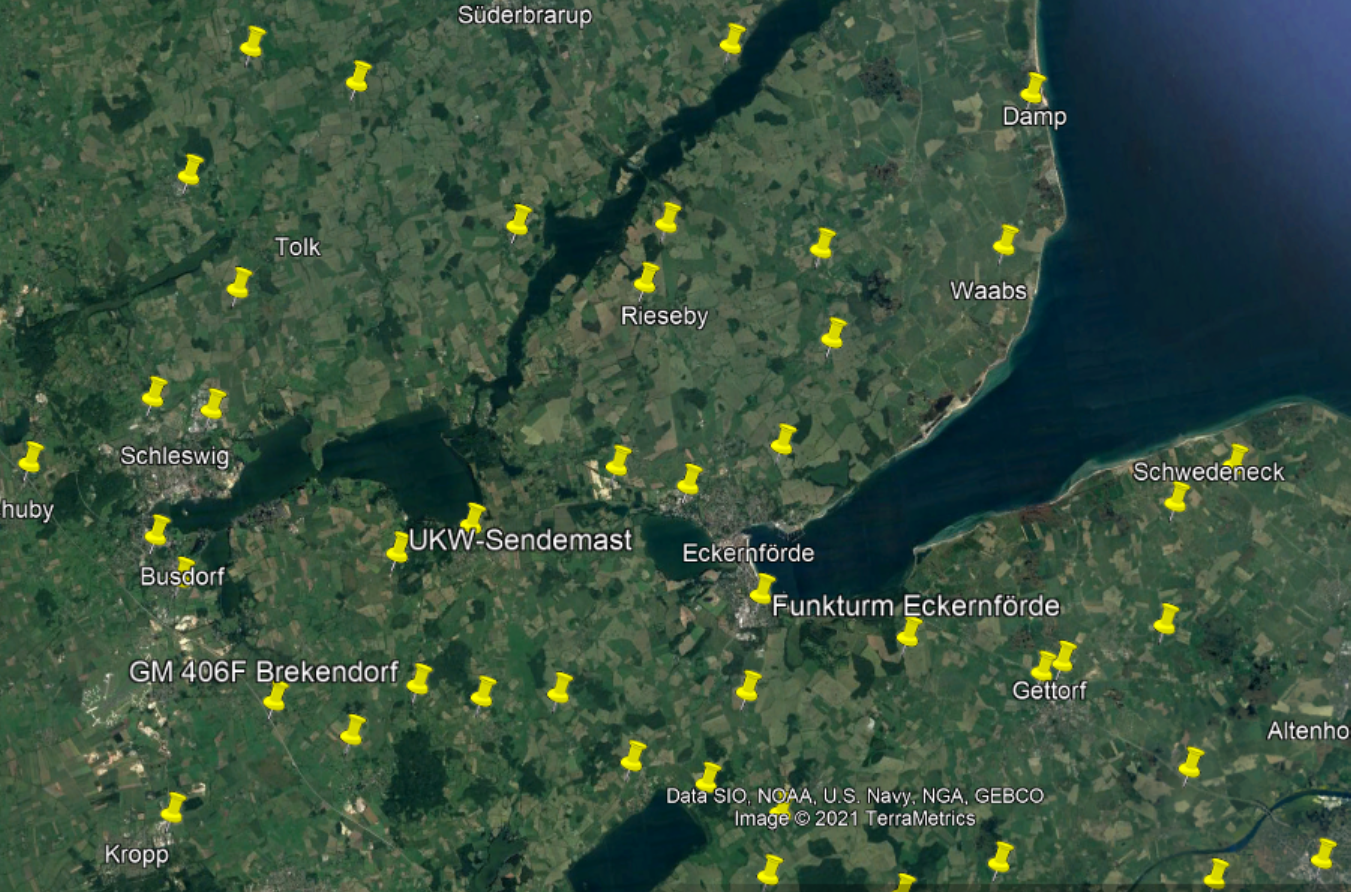
I pointed Overpass at the area around Eckernförde and this is what it found when I ran the towers query.:
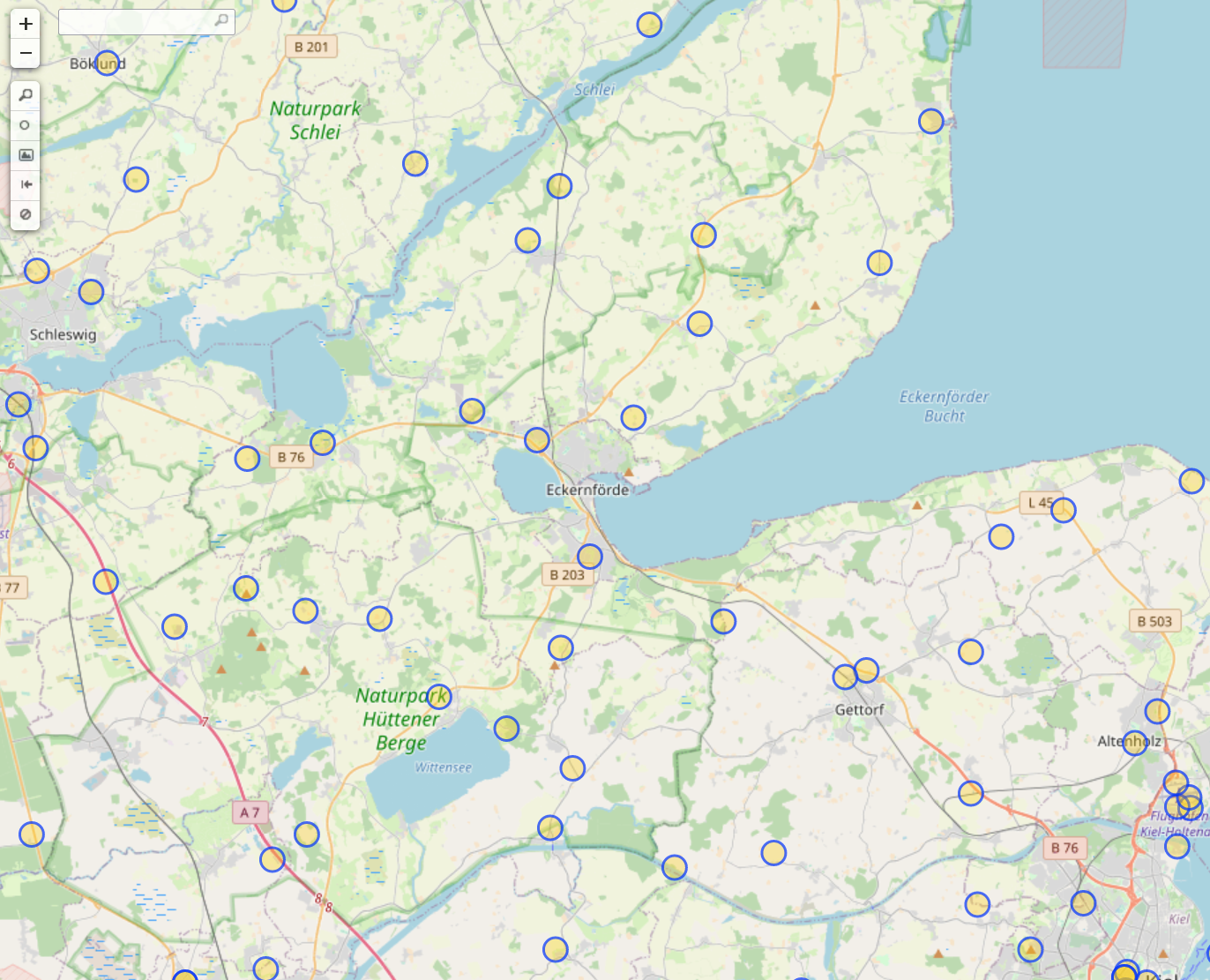
It is very likely that the cell tower Fiete was near is represented by one of the 72 circles on the map. This is certainly much easier to work through than thousands of cell masts, but it would still be time consuming and dull. We need some additional automation to review all these possible locations very quickly.
Speed and Scale With Google Earth
Google Earth Pro has a feature that allows users to make virtual tours of different points on the Earth’s surface by moving between a set of KML markers at a predetermined speed. You’ve probably seen this feature used in news reports where Google Earth is used. We can repurpose this tool for geolocation by getting Google Earth to fly between possible cell tower locations at high speed so we can see what each place looks like from the air. This is much faster than working through each location manually with Google Maps / Street View / Mapillary to see if it fits.
To do this first export the Overpass Turbo results as a KML file so that Google Earth can read it. Go to Export and click download as KML. The file will be saved as export.kml by default.
Next open up Google Earth Pro (you need the desktop version to do this, not the web version). Go to File and then Open the KML file you just downloaded. Create a folder for it in the Places tab. In this example I called my folder Cell Mast Tour.
Notice all the cell sites are now loaded directly into Google Earth. This will make verification much easier.
Next we need to set this up for a high speed verification tour. Go to Tools > Options > Touring. The menu looks something like this:
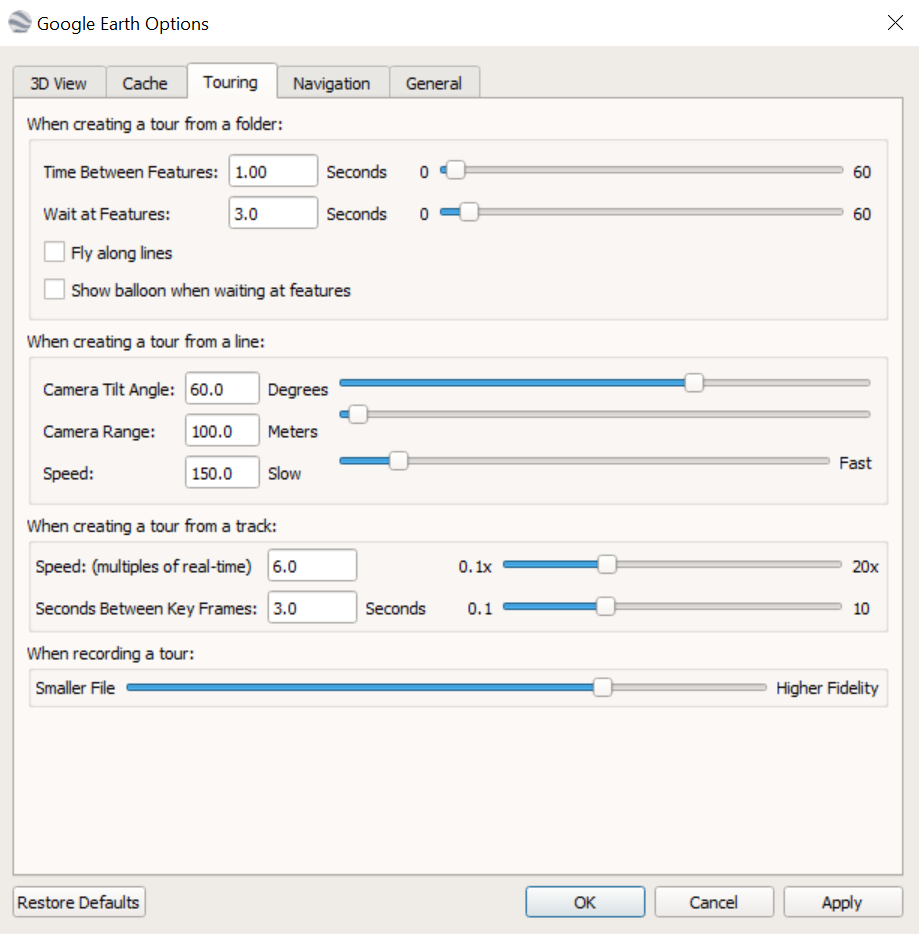
The only settings to change here are Time Between Features and Wait At Features. The first setting determines how long Google Earth takes to move from one point to the next, while the second decides how long to spend at each location. Three seconds might not seem like much but it is often enough to quickly assess whether a location is viable or not. You can always adjust the time delays or pause the tour if you want to inspect further. The mathematicians among you will realise that it will now only take 4.8 minutes to review all 72 possible cell mast locations near Eckernförde, and even less if we find the right one along the way. This is infinitely more efficient than doing things manually.
To launch the tour click on the Play Tour icon below the places menu:
Get ready to verify! There are controls in the bottom left corner that you can use to pause or reverse the video if you want to look at something in more detail. If this all gets too fast then we can slow things down but we should be confident in the data we have gathered so far.
We know that the cell mast we are looking for has a small cabin at the bottom, is next to a small road, and behind it there is some kind of facility with six floodlights. Any location that Google Earth takes us to that does not match all of these features can be immediately discounted with no further research required. With a little practice three seconds is generally plenty of time to do this. Here are a couple of examples from this dataset:
This mast is not in a field or next to a road. Immediately discounted.

This mast is in woods, not an open field, and it is not next to a road. Immediately discounted.
And so on, and so on…you can see how it is possible to work through these quite quickly. Even with a few pauses for further examination we can work through all 72 possible sites in less than quarter of an hour.
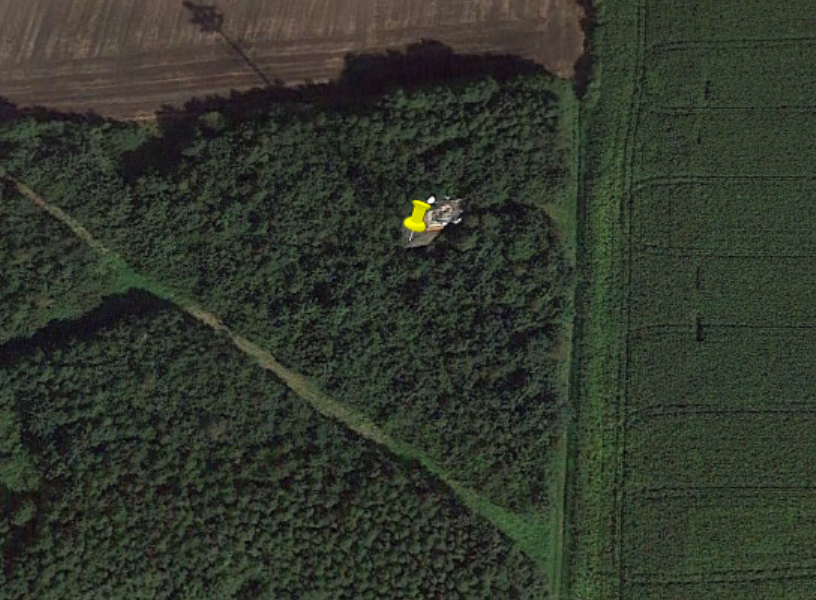
Very soon we find a site that looks much more promising:

Cell mast – check. Next to a road – check. Cabin at the base of the mast – check…and six floodlights visible behind the mast – check!
The correct location for the cell mast is here, just outside Waabs, Schleswig-Holstein, Germany.
We still need to verify the location as best as we can. There is no Street View coverage of this part of Germany, but Mapillary has captured the location. It is just about possible to make out the floodlights (red box) behind the cell tower (green box) in this blurry image take at the location. The road markers (blue box) are also present.

A search with Google Maps reveals this image of the location taken from the opposite direction to where Fiete was facing. By comparing it with the original we can see the road, cell tower, and floodlights all match.


If there was any doubt, we can also now confirm that the silo Fiete photographed on 4th October is here, and the beach he photographed on October 7th is probably around here somewhere, looking across the Eckernförder Bucht.
Who Was The Senior Commander?
We already have a probable plane (C-160 50+40) and we have also positively identified the location where Fiete was when he saw it. By working through the intelligence cycle we have turned what was initially quite a daunting search into something that is now very focused. We have already used Fiete’s Instagram to plot his timeline for the week leading up to the quiz and used it to successfully find the location. Now we just need to plot an overlapping timeline for C-160 50+40 and where its timeline and location intersects with Fiete’s, we will have found the correct mission. Once we have the correct mission then we can try to find the commander.
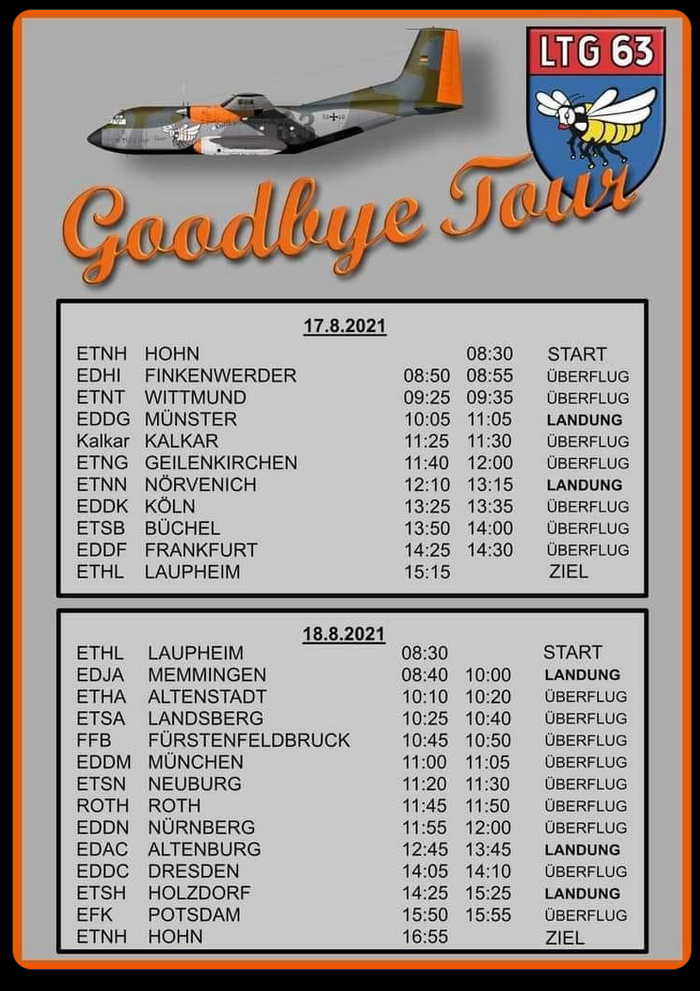
A few people who attempted to identify the specific flight fell into the trap of availability error. Availability error is a form of investigative bias where we tend to favour the data that is most readily presented to us, even if it is not right. Researching the history of C-160 50+40 showed that it embarked on a “Goodbye Transall” tour around northern Germany in June, and a follow-up tour around southern Germany in August. The high amount of information and publicity available about these specific flights crowded out lots of other useful information and although it was tempting to assume that Fiete saw the C-160 on a farewell flight, it is clear from his photo that this cannot be the case. The harvested field and trees that are starting to turn yellow should indicate this is not the peak of summer, and so Fiete did not witness one of the C-160 farewell flights.

A second assumption people made (including me at first) was about the commander of the operation. It is easy to find out from Wikipedia or the official Bundeswehr site that Markus Kleinbauer is the commander of the C-160 unit (LTG63), so although he may be in charge if the unit in a general sense, the challenge is to find out who the senior commander was for this specific mission. Details are important!
So that accounts for some of the wrong answers – but how do we find the right one? Remember that since we can be sure Fiete and the plane were in the same place at the moment the photo was taken, we just need to find where their timelines and locations overlap. We already know Fiete was in the Waab/Eckernförde area in the days leading up to 8th October, but a week before on 30th September he was in his usual location of Hamburg. So for Fiete’s timeline we can include 1st-8th October as the widest possible time period for when he might have been in the Eckernförde area.
This means we only need to be concerned with the movements of the C-160 within this time frame. Anything outside of these parameters is irrelevant. If a C-160 was somewhere at a time when Fiete was not near Eckernförde, we don’t care because it cannot be the right answer.

To construct a timeline for C-160 50+40 we can continue to search through resources generated by the planespotting community. Scramble is silent about C-160 movements during this time period, but Planespotters.net and Airplane Pictures are more helpful. From these sites we learn that 50+40 was at Münster Osnabrück airport on 6th October and that the day before it had flown to Chopin Airport in Warsaw, Poland. I considered whether Fiete had seen the plane on its way back from Warsaw, since in the image it is flying from the east roughly towards its home base at Hohn.
However further research led me to this image of 50+40, which stated that the plane returned to Münster Osnabrück after it went to Warsaw (i.e. without going back to Hohn first), so it would not make sense that Fiete saw the return flight from Warsaw when he was out near Waab.
None of these sources yet provide a satisfactory answer that ties in with what he have found so far, so either our hypothesis is wrong or we need to keep looking. Instead of focusing only on planespotting sites, why not search the largest repository of publicly-uploaded photos that has ever existed: Instagram?
There is an active planespotting community on Instagram, so by searching for hashtags relevant to the C-160 it is possible to find a lot of photos of interest. Hashtags like #c160, #retrobrummel, #ltg63 and #goodbyetransall all link to hundreds of images of the C-160. It is hard to conduct very granular searches on Instagram, so manually reviewing images is often necessary.
I found the #goodbyetransall hashtag quite helpful for documenting the past few weeks of C-160 movements. It is also clear that there is far more information available on Instagram than most of the planespotting sites. After flicking through dozens of photos, I came across this.
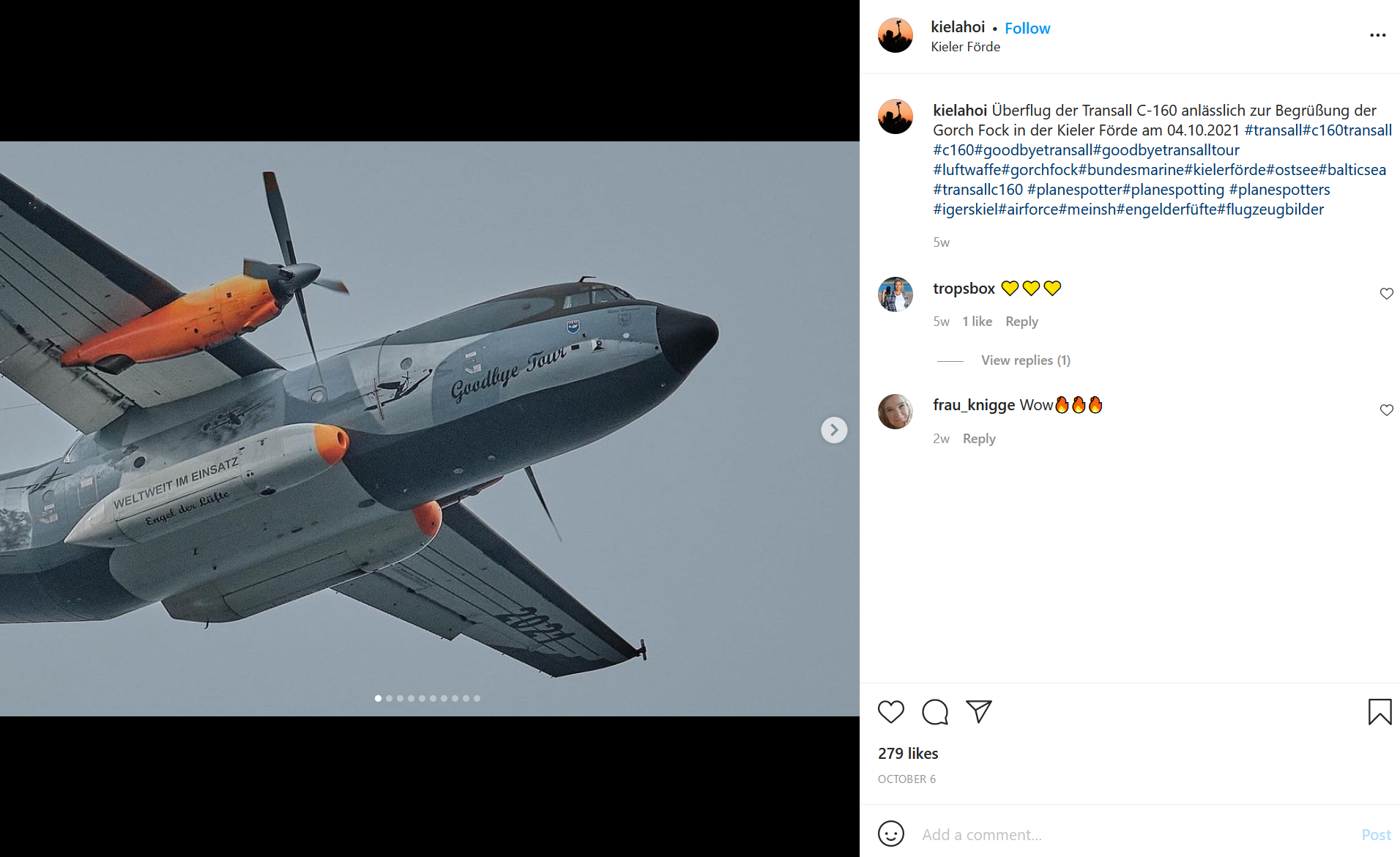
The account Kielahoi states that it is located in Kiel Bay – which is not that far from Fiete’s location at Waab. The account says that on 4th October the C-160 performed a flypast to greet the Gorch Fock in Kiel Ford as it returned to the harbour. The date and place align with Fiete’s timeline and location in a way that the trips to Poland and Münster do not, so we need to explore it further. We are getting close now!

After a little more Instagram research into the C-160 and the Gorch Fock, we hit the jackpot:
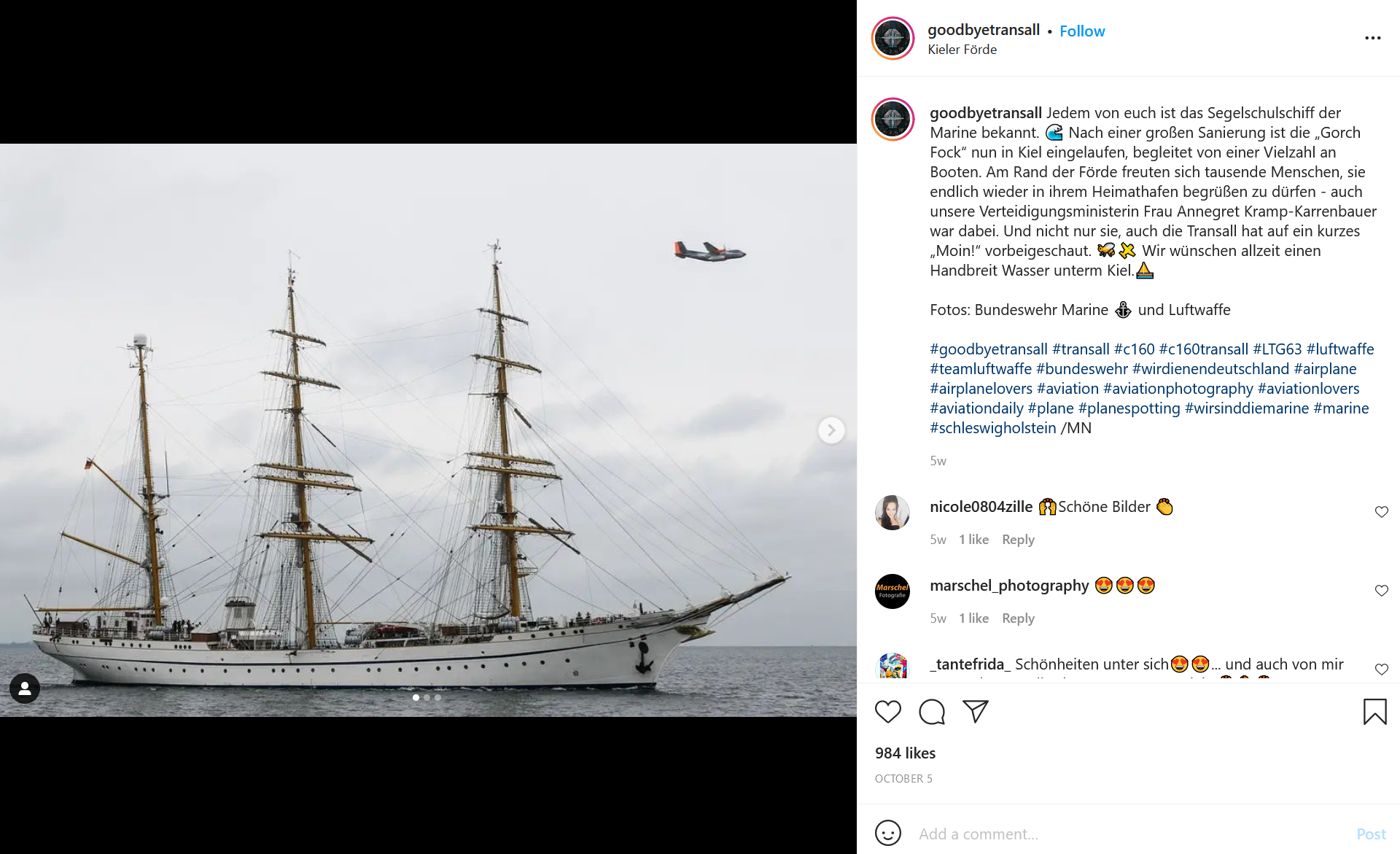
The @goodbyetransall account reports that the C-160 overflew the ship Gorch Fock as it was welcomed back to Kiel harbour after a period of restoration. If you don’t know any German already, then running this text through Google Translate will tell you that the German defence minister Annegret Kramp-Karrenbauer was present for the homecoming – so she is technically the highest in command for this particular operation. The official Bundeswehr article about the homecoming also has a picture of the event and confirms that Vice-Admiral Kay-Achim Schönbach was also present alongside the defence minister.
The event was also covered by the local news, which captured the event on video:
So we have managed to answer all three of Fiete’s questions. There is no doubt that Timmi Allen’s image enhancement helped to identify the C-160 with the unique orange tail and that this made things much faster – but what if we hadn’t had access to this? By being thorough with the parameters we set around the location and timeline, there is no other C-160 in the GAF fleet that is so strongly associated to the right location at the right time.
It is highly likely we would have been able to positively identify 50+40 by a process of elimination since there are no other candidates in the C-160 fleet that match all the criteria, but Timmi definitely made this quicker.
In the same way there is no other C-160 activity linked to the Waab/Eckernförde area in the time Fiete was there other than this mission to welcome the Gorch Fock home, so we can be confident it is the right mission in the absence of any other evidence.
If you enjoyed this write up then you might also be interested in my previous Quiztime write-ups, click here.


My jaw kept dropping lower and lower as I read on. Sherlock Holmes would have given up before the 1st question.
W
T
F
Geweldig werk: wat een mooie uitkomst van een onmogelijke opgave, zo leek het….
This is an amazing read and and even more amazing research. Thanks!
Thanks Wolfgang!
Wow. Just, wow. Kudos.
I was intrigued if us mere mortal non-programmers could also harness AI like Timmi Allen to enhance image quality and stumbled upon Remini app for Android which gave me this (in case HTML is not allowed here, the image URL is https://bit.ly/3djsXD6):
Impressive, but not as good: did not pick up the gold marking on the tail fin. Then again: even my mother could use it, it’s so easy.